The factorial function,
n! = 1 . 2 . ... . n,
has many interesting properties. In this problem, we want to
determine the maximum number of integer terms (excluding 1) that
can be used to express n!. For example:
8! = 1 . 2 . 3 . 4 . 5 . 6 . 7 . 8 = 2 . 3 . 2 . 2 . 5 . 3 . 2 . 7 . 2 . 2 . 2 = 27 . 32 . 5 . 7
By inspection, it is clear that the maximum number of terms
(excluding 1) that can be multiplied together to produce 8! is
11.
The input for your program consists of a series of test cases
on separate lines, ended by end-of-file. Each line contains one
number, n,
2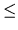 n
n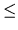 1000000.
1000000.
For each test case, print the maximum number of factors
(excluding 1) that can be multiplied together to produce n!.
Put the output from each test case on a separate line, starting
in the first column.
2
1000000
1996
5
8
123456
1
3626619
5957
5
11
426566
Miguel Revilla
2004-09-16