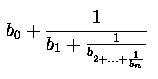
Continued Fractions 

Let b₀, b₁, b₂,..., b_n be integers with b_k > 0 for k > 0. The continued fraction of order n with coeficients b₁, b₂,..., b_n and the initial term b₀ is defined by the following expression

$${\frac{1}{b_1 + \frac{1}{b_{2 + \ldots + \frac{1}{b_n}}}}}$$

which can be abbreviated as [b₀;b₁,..., b_n].

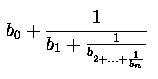
An example of a continued fraction of order n = 3 is [2;3, 1, 4]. This is equivalent to

$${\frac{1}{3 + \frac{1}{1 + \frac{1}{4}}}}$$

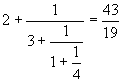
Write a program that determines the expansion of a given rational number as a continued fraction. To ensure uniqueness, make b_n > 1.

Input 

The input consists of an undetermined number of rational numbers. Each rational number is defined by two integers, numerator and denominator.

Output 

For each rational number given in the input, you should output the corresponding continued fraction.

Sample Input 

43 19
1 2

Sample Output 

[2;3,1,4]
[0;2]