Water Falls 

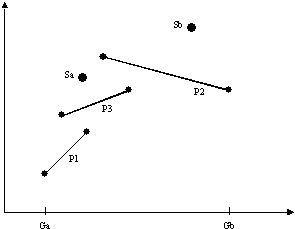
Consider the set of line segments P1, P2 and P3 of figure 1, representing the side view of a set of planes. What happens if some water falls (in the vertical direction and ignoring horizontal deviations created by kinetics) from source point Sa? It flows over the plane P3, to P1, finally falling on the ground at the point Ga. It is easy to see that, if the water is falling from source point Sb, then it hits the ground at the point Gb.

Given a list of lines segments and a list of source points, the proposed problem is to determine the corresponding falling points on the ground. To simplify the problem, it is assumed that neither horizontal lines nor crossing lines are given. Also no coincidences exist in the vertical projection of all points (the x coordinates of the end points and of the source points are all different).

Input 

The input begins with a single positive integer on a line by itself indicating the number of the cases following, each of them as described below. This line is followed by a blank line, and there is also a blank line between two consecutive inputs.

The input is a text file, containing several lines as follows.

The first line of the input contains the number NP (integer format) of line segments. It is followed by NP lines containing, each one, the coordinates of the two end points of a segment, in the sequence x₁ y₁ x₂ y₂, separated by single spaces. No order is supposed, for this case, between point 1 and point 2 and numbers are written in the integer format.

The next line is the number NS (integer format) of source points. It is followed by NS lines containing, each one, a pair of integer values x y, separated by a single space, which are the coordinates of the corresponding source point.

Output 

For each test case, the output must follow the description below. The outputs of two consecutive cases will be separated by a blank line.

NS lines of text containing, each one, the coordinate x (integer format) of the corresponding falling point G. The output values must keep the input order.

Sample Input 

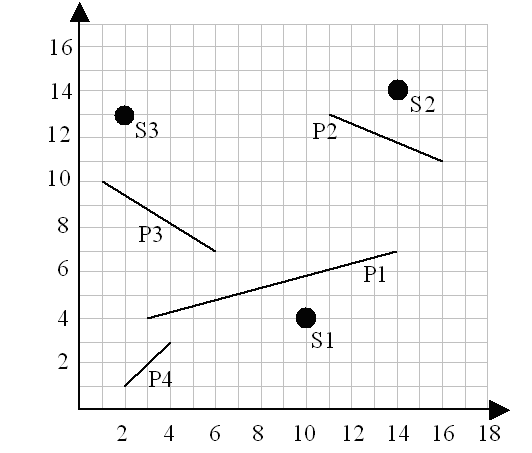
1

4
14 7 3 4
11 13 16 11
1 10 6 7
2 1 4 3
3
10 4
14 14
2 13

Sample Output 

10
16
2

Note: The picture below corresponds to the sample input.