Buddy Memory Allocator 

Memory management, specially memory allocation to processes, is a fundamental issue in operating systems. A fixed partitioning scheme limits the number of active processes and may use space inefficiently if there is a poor match between available partition sizes and process sizes. A dynamic partitioning scheme is more complex to maintain and includes the overhead of compaction. An interesting compromise is the buddy system.

In a buddy system, the entire memory space available for allocation is initially treated as a single block whose size is a power of 2. When the first request is made, if its size is greater than half of the initial block then the entire block is allocated. Otherwise, the block is split in two equal companion buddies. If the size of the request is greater than half of one of the buddies, then allocate one to it. Otherwise, one of the buddies is split in half again. This method continues until the smallest block greater than or equal to the size of the request is found and allocated to it.

In this method, when a process terminates the buddy block that was allocated to it is freed. Whenever possible, an unnallocated buddy is merged with a companion buddy in order to form a larger free block. Two blocks are said to be companion buddies if they resulted from the split of the same direct parent block.

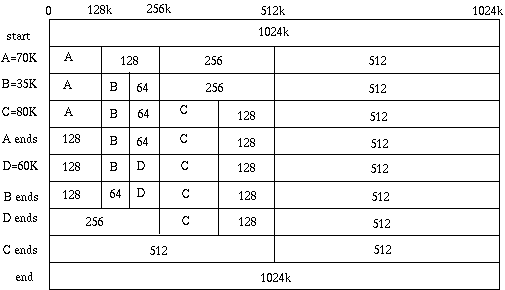
The following figure illustrates the buddy system at work, considering a 1024k (1-megabyte) initial block and the process requests as shown at the left of the table.

Your task is to implement a buddy memory manager and simulate it at work. You will be given the upper and lower sizes admissible for blocks in the system and a list of requests. A request is made for a process and it may either be for a block of a certain size or just an indication of termination. Requests should be attended in a firstcome firstserved basis. After serving all requests, your program should display the state of the buddy system at that point, indicating which processes are in memory and which blocks are free.

Notice that, whenever there is a request that corresponds to a block of size s, your program should select the block of that size that was most recently declared free. Furthermore, when a block is split in two, the left-one (lower addresses) should be selected before the right-one.

You can assume that the list of requests is such that all requests can always be served. In other words, you can make the following assumptions: no process will request more than the available memory; processes are uniquely identified while active; and no request for process termination is issued before its corresponding request for memory allocation.

Input 

The input begins with a single positive integer on a line by itself indicating the number of the cases following, each of them as described below. This line is followed by a blank line, and there is also a blank line between two consecutive inputs.

The first line of input consists of two numbers, U and L, that determine the upper (2^Uk) and lower (2^Lk) block sizes admissable. You can assume U > L > 0. The following input lines are requests being made, one per line. A request is defined by two values, P and S, where P is a capital letter that identifies the process associated with the request, and S ($\geq$ 0) is a number. If S > 0 then it is a memory block request; Otherwise (S = 0) it is a request indicating that process P has terminated.

Output 

For each test case, the output must follow the description below. The outputs of two consecutive cases will be separated by a blank line.

The output must list the state of the buddy immediatly after having served the last request. This corresponds to listing the processes still in memory, if any, and the free blocks (holes) available. Processes and holes must be listed in a left to right order as you traverse the buddy (i.e. from lower addresses towards upper memory addresses). The output format for processes is P : S, P is the process identifier and S its size, and for holes is Hole:S where S is the size of the free block.

Sample Input 

1

10 4
A 70
B 35
C 80
A 0
D 60
B 0

Sample Output 

Hole:128
Hole:64
D:60
C:80
Hole:128
Hole:512