| Petri Net Simulation |

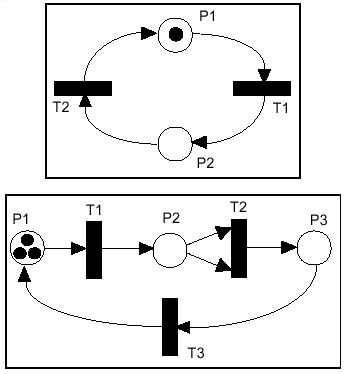
In the first Petri net above, there are two places (P1 and P2) and two transitions (T1 and T2). P1 initially has one token; P2 has none. P1 is an input place for transition T1, and P2 is an output place for T1. In the second example there are three places and three transitions, with three tokens in P1. T2 has two input places, both of which are P2.
In the top example only T1 is enabled. When it fires one token is removed from P1, and one token is added to P2. Then T2 is enabled. When it fires one token is removed from P2, and one token is added to P1. Clearly this Petri net will repeat this cycle forever.
The bottom example is more interesting. T1 is enabled and fires, effectively moving a token to P2. At this point T1 is still the only enabled transition (T2 requires that P2 have two tokens before it is enabled). T1 fires again, leaving one token in P1 and two tokens in P2. Now both T1 and T2 are enabled. Assume T2 fires, removing two tokens from P2 and adding one token to P3. Now T1 and T3 are enabled. Continuing until no more transitions are enabled, you should see that only one token will be left in P2 after 9 transition firings. (Note that if T1 had fired instead of T2 when both were enabled, this result would have been the same after 9 firings.)
In this problem you will be presented with descriptions of one or more Petri nets. For each you are to simulate some specified number of transition firings, NF, and then report the number of tokens remaining in the places. If the net becomes dead before NF transition firings, you are to report that fact as well.
The negative numbers in the list will represent the input places, so the number - n indicates there is an input place at n. The positive numbers in the list will indicate the output places, so the number p indicates an output place at p. There will be at least one input place and at least one output place for each transition. Finally, after the description of all NT transitions, there will appear an integer indicating the maximum number of firings you are to simulate, NF. The input will contain one or more Petri net descriptions followed by a zero.
The input data will be selected to guarantee the uniqueness of the correct output displays.
2 1 0 2 -1 2 0 -2 1 0 100 3 3 0 0 3 -1 2 0 -2 -2 3 0 -3 1 0 100 3 1 0 0 3 -1 2 3 0 -2 1 0 -3 1 0 1 0
Case 1: still live after 100 transitions Places with tokens: 1 (1) Case 2: dead after 9 transitions Places with tokens: 2 (1) Case 3: still live after 1 transitions Places with tokens: 2 (1) 3 (1)