Integral Determinant 

Write a program to find the determinant of an integral square matrix. Note that the determinant of a square matrix can be defined recursively as follows: the determinant of a 1$\times$1 matrix M = (a_1,1) is just the value |M| = a_1,1; further, the determinant of an $n \times n$ matrix is

$$\vert M\vert = \sum_{i=1}^n (-1)^{i+1} \cdot \vert M_{1,j}\vert.$$

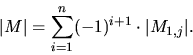
Here the notation M_1,i is the $(n-1) \times (n-1)$ matrix by removing the first row and the i^th column of the original $n \times n$ matrix M.

A straightforward method of calculating the determinant of an $n \times n$ matrix by the recursive method will end up with n! multiplications, a very time-consuming algorithm. To give you a feeling about this, note that 15! = 1,307,674,368,000. To reduce the time complexity, there are two ways of modifying the original matrix for easier computation.

1.

Exchanging two columns (or rows) of a matrix will change the sign of the determinant; for example

$$\left\vert \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array}\rig... ...ert \begin{array}{cc} 2 & 1 \\ 4 & 3 \end{array}\right \vert$$

2.

Multiplying one column by any constant, and add them to another column will not change the value of the determinant; for example:

$$\left\vert \begin{array}{ccc} 2 & 1 & 3 \\ 4 & 5 & 6 \\ 7 ... ... 4 \times 2 \\ 7 & 8 & 9 + 7 \times 2 \end{array}\right \vert$$

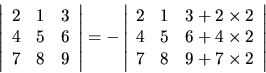
Using the above methods, you shall be able to write a program for computing the determinants of matrices, even for a size like 30$\times$30, very efficiently. Below is an example to show how this can be done:

$$\left\vert \begin{array}{ccc} 2 & 3 & 5 \\ 1 & 6 & 7 \\ 4 ... ... 1 & 1 & 2 \\ 5 & 5 & 1 \\ 1 & 4 & 4 \end{array}\right \vert$$

$$=- \left\vert \begin{array}{ccc} 1 & 1-1 & 2 - 1 \times 2 \\... ...begin{array}{cc} 0 & -9 \\ 3 & 2 \end{array}\right \vert =-27$$

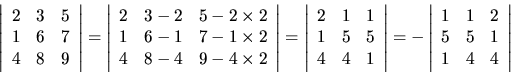
Note that the answer shall be an integer. That is, all the operations needed are just integer operations; by reducing to floating numbers would result in the round-off errors, which will be considered as the wrong answer. Do not worry about the problem of integral overflows problem. You can assume that the given data set will not cause the integer overflow problem. What is emphasized here is the required integer precision. Anyway use of floating numbers is not forbidden.

Input 

em Several sets of integral matrices. The inputs are just a list of integers. Within each set, the first integer (in a single line) represents the size of the matrix, n, which can be as large as 30, indication an $n \times n$ matrix. After n, there will be n lines representing the n rows of the matrix; each line (row) contains exactly n integers. Thus, there is totally n² integers for the particular matrix. These matrices will occur repeatedly in the input as the pattern described above. An integer n = 0 (zero) signifies the end of input.

Output 

For each matrix of the input, calculate its (integral) determinant and output it in a line. Output a single star (*) to signify the end of outputs.

Sample Input 

2
5 2
3 4
3
2 3 5
1 6 7
4 8 9
0

Sample Output 

14
-27
*