Exponential Function

Time limit: ? seconds
Memory limit: 64 megabytes

In the course of Linear Algebra, the following theorem is proved:

Theorem. Let A be a square matrix of size n with entries in in $\mathbb C$ . There are square matrices T and J of size n such that

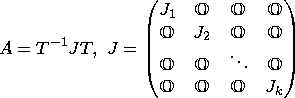
$$ A=T^{-1}JT,\ J= \left( \begin{matrix} J_1&\mathbb O&\mathbb O&\mathbb O\\ \mathbb O&J_2&\mathbb O&\mathbb O\\ \mathbb O&\mathbb O&\ddots&\mathbb O\\ \mathbb O&\mathbb O&\mathbb O&J_k \end{matrix} \right) $$
where Ji are Jordan cells:
$$ J_i=\left( \begin{matrix} \lambda_i&1&0&0&\dots&0\\ 0&\lambda_i&1&0&\dots&0\\ \ddots&\ddots&\ddots&\ddots&\ddots&\ddots\\ \ddots&\ddots&\ddots&\ddots&\ddots&\ddots\\ 0&\dots&\dots&\dots&\lambda_i&1\\ 0&\dots&\dots&\dots&\dots&\lambda_i\\ \end{matrix} \right) $$
Here $\lambda_i$ is an eigenvalue of A.

The decomposition $A=T^{-1}JT$ , where J is of the form described above, is called a Jordan decomposition of A. The Jordan decomposition of a matrix may fail to be unique.

Given a matrix A, we can define the matrix exp A in the following way: if $A=T^{-1}JT$ is a Jordan decomposition of A, then $\exp A=T^{-1}J^\prime T$ ,

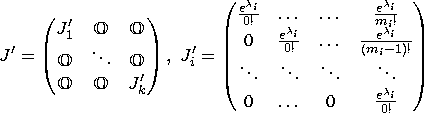
$$ J^\prime= \left( \begin{matrix} J_1^\prime&\mathbb O&\mathbb O\\ \mathbb O&\ddots&\mathbb O\\ \mathbb O&\mathbb O&J_k^\prime \end{matrix} \right),\ J_i^\prime = \left(\begin{matrix} {e^{\lambda_i}\over 0!}&\dots&\dots&{e^{\lambda_i}\over m_i!}\\ 0&{e^{\lambda_i}\over 0!}&\dots&{e^{\lambda_i}\over (m_i-1)!}\\ \ddots&\ddots&\ddots&\ddots\\ 0&\dots&0&{e^{\lambda_i}\over 0!} \end{matrix}\right) $$
Here mi is the size of Ji. If $k\leq l$ , then the number in the kth row and lth column of $J_i^\prime$ is
$$ j_{kl}={e^{\lambda_i}\over (l-k)!}, $$
otherwise it is 0.

It can be proved that exp A is independent of the Jordan decomposition of A used. It can also be proved that if A is real-valued, then exp A is also real-valued. Your task is: given a matrix A, compute exp A.

For example, if

$$ A=\left(\begin{matrix} 3&0\\ 1&3 \end{matrix}\right), $$

then

$$ J = \left(\begin{matrix} 3&1\\ 0&3 \end{matrix}\right),\ T = \left(\begin{matrix} 1&1\\ 1&0 \end{matrix}\right),\ J^\prime = \left(\begin{matrix} e^3&e^3\\ 0&e^3 \end{matrix}\right)$$

and

$$ \exp A = \left(\begin{matrix} e^3&0\\ e^3&e^3 \end{matrix}\right)\approx \left(\begin{matrix} 20.086&0\\ 20.086&20.086 \end{matrix}\right) $$

Input

The first line of the input contains the number of the test cases, which is at most 15. The descriptions of the test cases follow. The first line of a test case description contains one integer N (1 ≤ N ≤ 8), denoting the size of the matrix A. Each of the next N lines contains N integers separated by spaces, describing the matrix A. It is guaranteed that the entries of A are between 0 and 5. The test cases are separated by blank lines.

Output

For each test case in the input, output N lines, each containing N integers separated by spaces, describing the matrix exp A. The numbers must have at least three digits after the decimal point. Print a blank line between test cases.

Examples

InputOutput 
2

2
3 0
1 3

2
1 5
0 1

20.086 0.000
20.086 20.086

2.718 13.591
0.000 2.718