Problem B
Tangents
Input: standard input
Output: standard output
Time Limit: 2 seconds
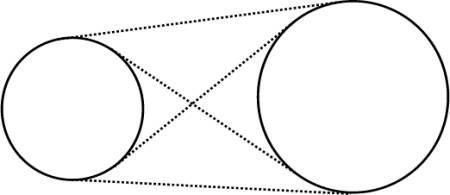
You can see in the pictures below that two different circles can have at most four common tangents. Given the center and radius of two circles your job is to find the length of their common tangents and also the points where they touch the two circles.
Input
The input file contains several lines of inputs.
Each line contains six integers x1 (-100<=x1<=100), y1 (-100<=y1<=100), r1 (0<r1<=200), x2 (-100<=x2<=100), y2 (-100<=y2<=100), r2 (0<r2<=200). Here (x1, y1) and (x2, y2) are the coordinates of the center of the first circle and second circle respectively, r1 is the radius of the first circle and r2 is the radius of the second circle.
Input is terminated by a line containing six zeroes.
Output
For each line of input you should produce one of more lines of output. The description of this output is given below.
First line of the output for each line of input contains an integer n, which denotes the number of different tangents between the two circles. If there is infinite number of tangents between the two circles then the value of n should be –1. If n is positive then next n lines contains the description of each tangent. The description of the tangent contains five floating-point numbers Sx, Sy, Tx, Ty, L in a single line. Here (Sx, Sy) is the point at which the tangent touches the first circle and (Tx, Ty) is the point where the tangent touches the second circle and L is the length of the tangent. All the floating-point numbers have five digits after the decimal point. Errors less than 2*10-5 will be ignored. The tangents should be printed in ascending order of Sx and in case of a tie they should be printed in ascending order of Sy.
Sample
Input Output for Sample Input
|
10 10 5 20 20 5 10 10 10 20 20 10 10 10 5 20 10 5 0 0 0 0 0 0 |
4 6.46447 13.53553 16.46447 23.53553
14.14214 10.00000 15.00000 20.00000 15.00000
10.00000 13.53553 6.46447 23.53553 16.46447
14.14214 15.00000 10.00000 15.00000 20.00000
10.00000 2 2.92893 17.07107 12.92893 27.07107
14.14214 17.07107 2.92893 27.07107 12.92893
14.14214 3 10.00000 5.00000 20.00000 5.00000 10.00000 10.00000 15.00000 20.00000 15.00000
10.00000 15.00000 10.00000 15.00000 10.00000
0.00000 |
Problem setter: Shahriar
Manzoor. Member of Elite Problem Setters’ Panel
Special Thanks: Derek
Kisman, Member of Elite Problem Setters’ Panel