Problem H
Square Puzzle
Input: Standard Input
Output: Standard Output
Time Limit: 3 Seconds
Given the pieces of a puzzle, determine if they can be put together so they form a square of a given size. The pieces may be rotated but not flipped, and all pieces must be used. Pieces may of course not overlap.
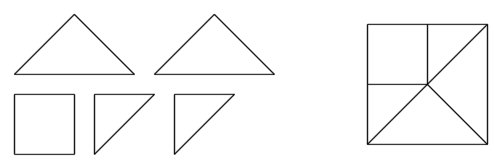
The pieces to the left can be moved and rotated so they form the square to
the right.
The shape of the pieces will be
given as simple polygons. All vertices will have integer coordinates, and will
be given in counter-clockwise direction. The sides of the pieces will either be
horizontal, vertical or diagonal.
Input
The first line in the inputer contains an integer P, the number of puzzles to follow (at most 20). Each puzzle starts with a line containing two integers, n and m (both between 1 and 6, inclusive). n is the number of pieces in the puzzle, while m is the length of the side of the square you want to create.
Then follows n lines, each describing a piece. Each
line starts with an integer k, the number of vertices in the polygon.
Then follows k pair of integers, the x- and y-coordinates
for the vertices. All coordinates in a particular puzzle will be between 0
and m, inclusive.
Output
For each puzzle, output on a single line either "yes" or "no", depending on whether you can form a m x m square using all the pieces.
Sample Input Output for Sample Input
25 64 0 0 3 0 3 3 0 33 0 0 3 3 0 33 0 0 3 3 0 33 0 0 6 0 3 33 0 0 6 0 3 33 45 1 0 3 0 3 3 2 4 1 43 0 0 2 0 1 15 1 0 3 0 3 3 2 4 1 4 |
yes
no |
Problemsetter: Jimmy Mårdell, Member of Elite
Problemsetters' Panel