A fraction h/k is called a proper fraction if it lies
between 0 and 1 and if h and k have no common factors.
For any natural number n >= 1, the Farey sequence of order
n, Fn, is the sequence of all proper fractions
with denominators which do not exceed n together with the
"fraction" 1/1, arranged in increasing order. So, for example,
F5 is the sequence:
1 1 1 2 1 3 2 3 4 1
-, -, -, -, -, -, -, -, -, -.
5 4 3 5 2 5 3 4 5 1
It is not clear exactly who first thought of looking at such
sequences. The first to have proved genuine mathematical results
about them seems to be Haros, in 1802. Farey stated one of Haros'
results without a proof in an article written in 1816, and when Cauchy
subsequently saw the article he discoverd a proof of the result and
ascribed the concept to Farey, thereby giving rise to the name
Farey sequence. Hardy in his A mathematician's
apology writes:
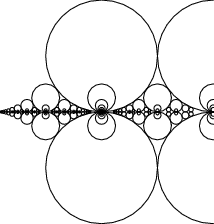
... Farey is immortal because he failed to understand a theorem which Haros had proved perfectly fourteen years before ...Surprisingly, certain simple looking claim about Farey sequences is equivalent to the Riemann hypothesis, the single most important unsolved problem in all of mathematics. Ford circles, see picture, provide a method of visualizing the Farey sequence.
But your task is much simpler than this.
For a given n, you are to find the k-th fraction in the sequence Fn. Input consists of a sequence of lines containing two natural numbers n and k, 1 <= n <= 1000 and k sufficiently small such that there is the k-th term in Fn. (The length of Fn is approximately 0.3039635n2). For each line of input print one line giving the k-th element of Fn in the format as below.
5 5 5 1 5 9 5 10 117 348 288 10000
1/2 1/5 4/5 1/1 9/109 78/197