It's a bird! It's a plane! It's coming right at us!
Although it sometimes seems like it, Superman can't fly (without a plane). Instead, he makes super-human leaps, especially over tall buildings. Since he never knows when he will need to catch a criminal, he can't register flight paths. To avoid hitting planes, he tries to keep his jumps as low to the ground as he can. Given a city-scape as input, find the angle and velocity of Superman's jump that minimizes his maximum altitude.
Recall that gravity provides an acceleration of 9.8 m/s2 downwards and the formula for Superman's vertical distance from his starting location is d(t)=v t + 0.5 a t2 where v is his initial velocity, a is his acceleration and t is time in seconds since the start of the leap.
Input consists of a sequence of city-scapes, each of the form
n
0 d1
h2 d2
:
h(n-1) d(n-1)
0 dn
Superman starts at ground level and leaps d1+...+dn metres, landing at ground level and clearing all of the buildings at heights h2 to h(n-1), each with the given widths. n will be at most 100.
Output is the angle and initial velocity that minimizes the height that Superman attains, both appearing on the same line. The values should be given to two decimal places and be accurate within 0.01 degrees or m/s, as appropriate.
3 0 5 10 5 0 5 5 0 10.5 20 11.5 25 10 10 15 0 7
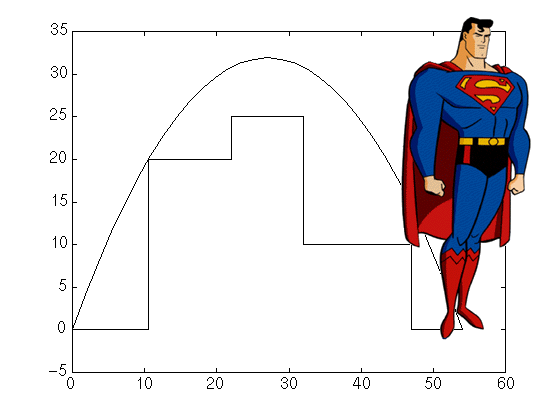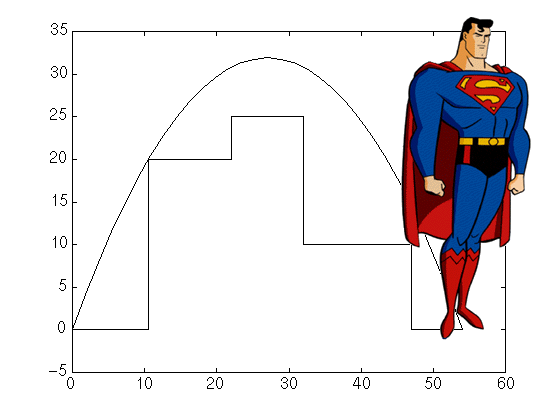
71.57 15.65 67.07 27.16