Problem A
The Kissing Circles
Input: standard input
Output: standard output
Time Limit: 2 seconds
Memory Limit: 32 MB
There
are some interesting figures below. You can see that we can put within a circle
one or more circles of equal radius. The important property of these circles is
that every consecutive circles touch each other. Given the radius R of the larger circle and the number
of small circles N of equal radius
inside,† you will have to find the radius
of the smaller circles r, the area
surrounded by the kissing small circles (light blue) I and the area outside the kissing small circles but inside the
larger circle (light green) E.
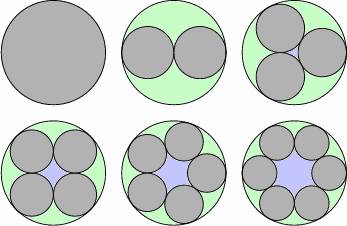
Fig: Figures for N = 1, 2, 3, 4, 5, 6
Input
The input file will contain several lines of inputs. Each line contains non-negative integers R(R<=10000) and N (1<=N<=100) as described before. Input is terminated by end of file.
Output
For
each line of input produce one line of output. This one line contains three
floating point numbers r, I and E as described before. The floating point numbers should have ten
digits after the decimal point. The output will be checked with special
correction programs. So you wonít have to worry about small precision
errors.
Sample Input
10 3
10 4
10 5
10 6
Sample
Output
4.6410161514 3.4732652470 107.6854162259
4.1421356237 14.7279416563 83.8264899217
3.7019190816 29.7315551092 69.1625632742
3.3333333333 45.6568837582 59.0628713615
(Math Loversí Contest, Problem Setter: Shahriar Manzoor, Thanks to Dr. Erich Friedman & Math world)