| Partial differential equations |
In engineering sciences, partial differential equations play an important and central role. For example, the temperature of a metal plate can be expressed as a partial differential equation if the temperature on the boundaries is known. This is called a boundary value problem.
Usually, it is not easy to solve these problems. Analytical solutions exist only in very special cases. But there are some more or less "good" numerical ways to solve boundary value problems.
We now will look at one method which works with finite difference approximations
for the derivatives of a function. For this approach, we do not look at
an analytical function u(x) but we are only interested in
the values of u at a finite set of discrete points ![]() . The distance between two adjacent
points,
. The distance between two adjacent
points, ![]() and
and ![]() , is constant:
, is constant: ![]() (cf. figure 1).
(cf. figure 1).
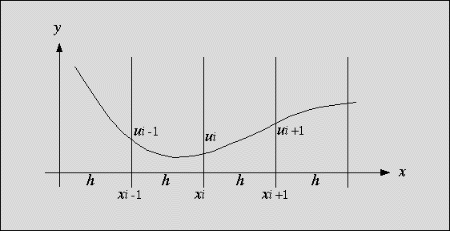
Figure: u(x) at some discrete points ![]()
The finite difference approximation of a first derivative of the function u(x) is
![]()
The second derivative is approximated by
![]()
This approximation works with 2-dimensional functions u(x,y) as well.
For simplicity we only work on square problems, i.e.
(x, y) is element of ![]() . Again, the area of the
function is discretized in a similar way:
. Again, the area of the
function is discretized in a similar way: ![]() ,
for some integer
,
for some integer ![]() . We only look at the values of u(x,y) at the
discrete points
. We only look at the values of u(x,y) at the
discrete points ![]() .
With this discretization, we have a function
.
With this discretization, we have a function ![]() as shown in figure 2:
as shown in figure 2:
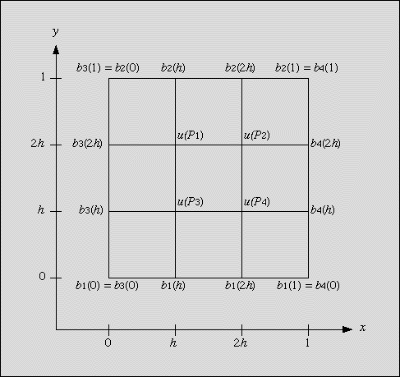
Figure: Function ![]() in the discretization area
in the discretization area
On the boundary, ![]() is given by 4 known functions:
is given by 4 known functions:

The points ![]() cover the inner points of the discretization
area, i.e. the area without the boundary. They are numbered from left to
right and from top to bottom like English text.
cover the inner points of the discretization
area, i.e. the area without the boundary. They are numbered from left to
right and from top to bottom like English text.
What we now want to do is to solve the poisson-equation in
the area ![]() :
:
![]()
with the above boundary conditions. f(x,y) is a given 2-dimensional function. With equation (2) and the above discretization, the poisson-equation can be approximated at
![]()
where ![]() is the function f(x,y), evaluated at the discrete
points
is the function f(x,y), evaluated at the discrete
points ![]() .
.
Formula (5) can be written in a more readable form, depending on the position of the discrete points:
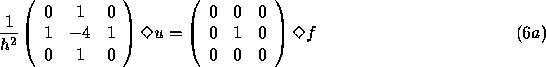
A similar equation, which we will use as an example below, is:
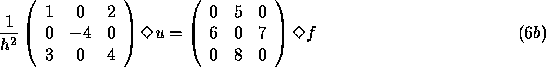
We call the ![]() matrix on the left hand side v and
the
matrix on the left hand side v and
the ![]() matrix on the right hand side g.
matrix on the right hand side g.
Now, equation (6b) can be formulated in every point of the discrete area of figure 2:
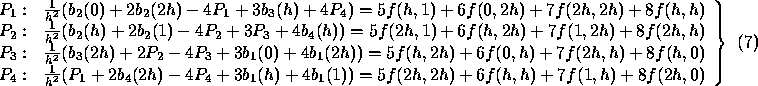
and (7) is a linear equation system for the values of u(x,y) at the
points ![]() and
and ![]() .
.
By rearranging and adding the terms on each line, the linear equation system can be formulated as:
![]()
where a is a ![]() matrix and b is a vector with 4 elements. Vector
z represents the unknown values of u(x,y) at the
points
matrix and b is a vector with 4 elements. Vector
z represents the unknown values of u(x,y) at the
points ![]() and
and ![]() .
.
You are to write a program that creates the linear equation system (7) in
the form (8) for any two matrices v and g (6). As input, the
two matrices v and g and the functions ![]() , and f
are given. Also, a parameter n is given as the number of discretization
intervals. Thus,
, and f
are given. Also, a parameter n is given as the number of discretization
intervals. Thus, ![]() . As the result, your program should calculate the
matrix a and the vector b. For this more general case, there
are
. As the result, your program should calculate the
matrix a and the vector b. For this more general case, there
are ![]() inner points and a and b must
be sized accordingly.
inner points and a and b must
be sized accordingly.
The input file consists of m tests. The number m is given
in the first line of the file. The first line of each test contains the
number n which gives the number of discretizations intervals as defined
above. You may assume that ![]() . Then the
. Then the ![]() matrices v
and g follow. The following four lines contain the functions
matrices v
and g follow. The following four lines contain the functions ![]() and
and ![]() , each
given as a vector of order n+1, containing the values for 0, h,
2h, ..., 1. Finally, the function f is given as a n+1 by n+1
matrix. Like the vectors before, it contains the values for
, each
given as a vector of order n+1, containing the values for 0, h,
2h, ..., 1. Finally, the function f is given as a n+1 by n+1
matrix. Like the vectors before, it contains the values for ![]() . Each row contains from left to right the
function values for increasing x values while each column contains
from top to bottom the function values for decreasing y values.
. Each row contains from left to right the
function values for increasing x values while each column contains
from top to bottom the function values for decreasing y values.
A vector occupies one line. Its values are given in ascending order, separated by a space. A n by n matrix occupies n lines. Its rows are given in ascending order as vectors, which occupy one line each. All values found in the input file are integer values.
For each test found in the input file, your program should output the matrices
a and b. Matrix a is a ![]() matrix (the discretization area (cf. figure 2) contains
matrix (the discretization area (cf. figure 2) contains ![]() inner points, which are unknown). The vector b is of order
inner points, which are unknown). The vector b is of order
![]() . They should be output in the same format as the
vectors and matrices in the input file. Your output should only contain
integer values. Note that the expression
. They should be output in the same format as the
vectors and matrices in the input file. Your output should only contain
integer values. Note that the expression ![]() yields
an integer number and that all other calculations can also be done using
integer numbers.
yields
an integer number and that all other calculations can also be done using
integer numbers.
1 3 1 0 2 0 -4 0 3 0 4 0 5 0 6 0 7 0 8 0 3 4 5 6 0 1 2 3 3 2 1 0 6 5 4 3 1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4
-36 0 0 36 0 -36 27 0 0 18 -36 0 9 0 0 -36 -35 -188 -189 -315